Relación entre la funcion Sigmoidea (logística o σ) y la Tangente Hiperbólica (TanH)

La función tanh (tangente hiperbólica) convierte cualquier valor al intervalo (−1,1)(-1,1).

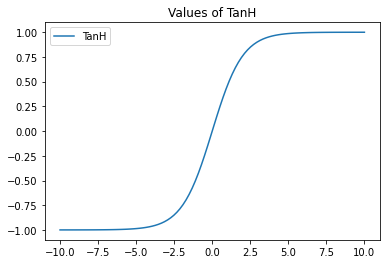
Es una función geométrica; al igual que tan(x)=cos(x)sen(x)tan(x)=\frac{cos(x)}{sen(x)}, tanhtanh se define a partir del coseno y seno hiperbólicos:

tanh(x)=cosh(x)senh(x)=ex−e−xex+e−x tanh(x)= \frac{cosh(x)}{senh(x)} = \frac{e^x-e^{-x}}{e^x+e^{-x}}

De esta forma, por ejemplo, tenemos:

tanh(0)=1−11+1=02=0 tanh(0)=\frac{1-1}{1+1}=\frac{0}{2}=0
tanh(1)=e−e−1e+e−1=2.353.08=0.76 tanh(1)=\frac{e-e^{-1}}{e+e^{-1}}=\frac{2.35}{3.08}=0.76
tanh(−1)=e−1−ee−1+e=−2.353.08=−0.76 tanh(-1)=\frac{e^{-1}-e}{e^{-1}+e}=\frac{-2.35}{3.08}=-0.76

Como vemos entonces, el balance de la función está en el valor 00, para el cual la salida es 0.50.5; valores mayores a 00 causan salidas mayores, y viceversa, y eso sucede de forma antisimétrica.

Vemos que en verdad es muy similar a la función SigmoidSigmoid. De hecho, con el siguiente gráfico podemos observar que TanHTanH es simplemente SigmoidSigmoid multiplicada por dos (para convertir el rango (0,1)(0,1) al rango (0,2)(0,2)) y luego restarle 1 (para convertir el rango (0,2)(0,2) al rango (−1,1)(-1,1)). Además, tenemos que multiplicar a xx por 2, para que la curva de ambas sea igual:

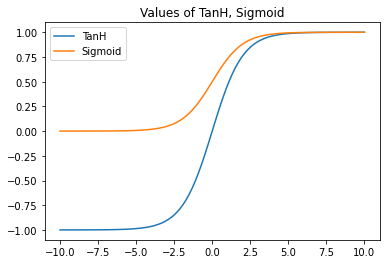
Por eso, vamos a definir a tanhtanh en base a SigmoidSigmoid:
tanh(x)=sigmoid(2x)∗2−1 tanh(x) = sigmoid(2x)*2-1

Podemos probarlo también. Para eso primero nos será útil saber que:

Sigmoid(x)=11+e−x=exex11+e−x=exex+1=ex+1−1ex+1=ex+1ex+1−11+ex=1−Sigmoid(−x)\begin{aligned} Sigmoid(x) &= \frac{1}{1+e^{-x}} \\ &= \frac{e^x}{e^x} \frac{1}{1+e^{-x}} \\ &= \frac{e^x}{e^x+1} \\ &= \frac{e^x+1-1}{e^x+1} \\ &= \frac{e^x+1}{e^x+1} - \frac{1}{1+e^{x}} \\ &= 1-Sigmoid(-x) \end{aligned}

Ahora si probemos que TanH(x)=2Sigmoid(x)−1TanH(x)=2 Sigmoid(x)-1

TanH(x)=ex−e−xex+e−x=exexex−e−xex+e−xMultiplicamos por 1 en forma de e−xe−x =e2x−1e2x+1Multiplicamos por e−x num. y denom. =1−ewew+1Definimos w=2x (ya se parece sospechosamente a Sigmoid) =1−ew+1−11+e−wSumamos y restamos 1=1+e−w−21+e−w=1+e−w1+e−w−21+ewSeparamos teˊrminos del num=1−21ew+1=1−2Sigmoid(w)Definicioˊn de Sigmoid=1−2(1−Sigmoid(−w))Sigmoid(x)= 1-Sigmoid(1-x)=1−2+2Sigmoid(−w))distributiva=2Sigmoid(−w)−1=2Sigmoid(−2x)−1w=2x\begin{aligned} TanH(x) &= \frac{e^x - e^{-x}}{e^x + e^{-x}}\\ &= \frac{e^x}{e^x} \frac{e^x - e^{-x}}{e^x + e^{-x}} & \text{Multiplicamos por 1 en forma de $\frac{e^{-x}}{e^{-x}}$ } \\ &= \frac{e^{2x}-1}{e^{2x}+1} & \text{Multiplicamos por $e^{-x}$ num. y denom. } \\ &= \frac{1-e^w}{e^w+1} &\text{Definimos $w=2x$ (ya se parece sospechosamente a $Sigmoid$) } \\ &= \frac{1-e^{w}+1-1}{1+e^{-w}} & \text{Sumamos y restamos 1} \\ &= \frac{1+e^{-w}-2}{1+e^{-w}} & \\ &= \frac{1+e^{-w}}{1+e^{-w}} - \frac{2}{1+e^{w}} & \text{Separamos términos del num}\\ &= 1 - 2\frac{1}{e^{w}+1} &\\ &= 1 - 2 Sigmoid(w) & \text{Definición de Sigmoid}\\ &= 1 - 2 (1-Sigmoid(-w)) & \text{Sigmoid(x)= 1-Sigmoid(1-x)}\\ &= 1 - 2 + 2 Sigmoid(-w)) & \text{distributiva}\\ &= 2 Sigmoid(-w) -1 &\\ &= 2 Sigmoid(-2x) -1 & \text{$w=2x$} \end{aligned}